8553. Компьютерная
сеть
В сети имеется n компьютеров, пронумерованных
от 0 до n – 1. Каждый компьютер, получив
сообщение, передает его другим компьютерам. При этом, если сообщение с
компьютера x может быть доставлено на компьютер y, это не
означает, что сообщение с компьютера y может быть отправлено обратно на
компьютер x.
Системные администраторы хотят определить минимальное
количество компьютеров, с которых необходимо отправить сообщение, чтобы оно
дошло до всех компьютеров в сети.
Кроме того, для повышения эффективности передачи
сообщений предполагается расширить сеть, добавив новые соединения между
некоторыми компьютерами. Это позволит добиться того, чтобы сообщение,
отправленное с любого компьютера, могло быть доставлено на любой другой.
Напишите программу, которая вычисляет:
·
Минимальное
количество компьютеров, с которых следует отправить сообщение, чтобы охватить
всю сеть.
·
Минимальное
количество новых соединений, которые следует добавить, чтобы сеть стала
полностью связной, то есть сообщение, отправленное с любого компьютера, могло
достичь любого другого.
Вход. Первая строка содержит два целых числа n (1 ≤ n ≤ 1600) и m (0 ≤
m ≤ 120000), задающих
количество компьютеров и число связей между ними. Каждая из следующих m строк описывает одну из имеющихся
связей. Первое число в строке – номер компьютера, отправляющего сообщение,
второе число – номер компьютера, принимающего сообщение.
Выход. Выведите в одной строке два целых числа:
·
Минимальное
количество компьютеров, которые необходимо использовать в качестве начальных
для распространения сообщения по всей сети;
·
Минимальное
количество дополнительных соединений, требуемых для того, чтобы сделать сеть
полностью связной, то есть чтобы сообщение, отправленное с любого компьютера,
могло достичь всех остальных.
|
Пример входа 1 |
Пример выхода 1 |
|
5 6 0 1 0 3 0 2 1 3 1 4 4 0 |
1 2 |
|
|
|
|
Пример входа 2 |
Пример выхода 2 |
|
6 12 0 1 0 2 1 0 1 2 2 0 2 1 3 4 3 5 4 3 4 5 5 3 5 4 |
2 2 |
РЕШЕНИЕ
графы - сильная связностть
Анализ алгоритма
Выделим в
графе компоненты сильной связности. Если граф
состоит из одной компоненты (то есть является сильно связным), то сообщение для
всей сети можно отправить из любого одного компьютера, при этом дополнительных
соединений не требуется (их количество равно 0).
Теперь
рассмотрим случай, когда граф не является сильно связным. Рассмотрим его
конденсацию. Для каждой компоненты сильной связности определим, существуют ли
входящие в нее и исходящие из нее ребра. Если в какую-либо компоненту нет
входящих ребер, то для рассылки сообщения по всей сети его необходимо отправить
из вершины, принадлежащей этой компоненте.
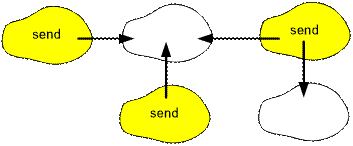
Например,
для приведенной ниже конденсации графа сообщение следует отправить с 3
компьютеров.
Для того чтобы сообщение, отправленное с любого
компьютера, могло достичь любого другого компьютера в сети, граф должен быть
сильно связным. Необходимо добавить в исходный граф минимальное количество
ребер, чтобы сделать его сильно связным.
Для каждой компоненты сильной связности графа должно
существовать как входящее в нее ребро, так и исходящее. Пусть:
·
с1 – количество компонент, не имеющих входящих ребер (на
рисунке с1 = 3);
·
с2 – количество компонент, не имеющих исходящих ребер
(на рисунке с2 = 2);
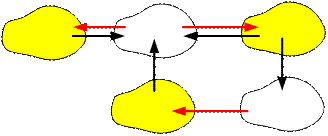
Тогда всегда можно добавить max(c1, c2)
ребер, чтобы сделать
граф сильно связным. В приведенном примере max(c1, c2) = max(3, 2) = 3. Таким образом,
для получения сильно связного графа достаточно добавить 3 ребра.
Пример
В первом тесте граф содержит
три компоненты сильной связности.
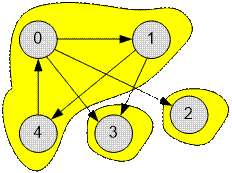
·
Одна компонента
не имеет входящих ребер: {0, 1, 4}, с1 = 1;
·
Две компоненты не
имеют исходящих ребер: {2}, {3}, с2
= 2;
Сообщение, которое должно
распространиться по всей сети, необходимо отправить из компонент, не имеющих
входящих ребер. В данном случае такая компонента одна – {0, 1, 4}. Сообщение
можно отправить из любой вершины этой компоненты (например, из 0, 1 или 4).
Для того чтобы сделать весь
граф сильно связным, необходимо добавить ребра, исходящие из вершин компонент
{2} и {3}. По крайней мере одно из этих ребер должно входить в компоненту {0, 1,
4}. Например, добавление следующих ребер сделает граф сильно связным:
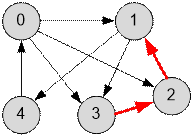
Реализация алгоритма
Входной граф храним в списке смежности g. Обратный граф (граф, в котором
изменены все направления ребер) храним списке смежности gr. Объявим также дополнительные
массивы.
vector<vector<int> > g, gr;
vector<int> used, top, color;
vector<int> in, out;
Функция dfs1 реализует поиск в глубину на входном
графе. В массив top
заносим последовательность вершин, в которой поиск в глубину завершает их
обработку.
void dfs1(int v)
{
used[v] = 1;
for (int to : g[v])
if (!used[to]) dfs1(to);
top.push_back(v);
}
Функция dfs2 реализует поиск в глубину на обратном графе. Все вершины,
которые будут пройдены в результате рекурсивного вызова функции dfs2,
принадлежат одной компоненте сильной связности. Красим все пройденные вершины
цветом с.
void dfs2(int v, int c)
{
color[v] = c;
for (int to : gr[v])
if (color[to] == -1) dfs2(to, c);
}
Основная
часть программы. Читаем входные данные. Строим обратный граф.
scanf("%d %d", &n, &m);
g.resize(n
+ 1);
gr.resize(n
+ 1);
for (i = 0; i < m; i++)
{
scanf("%d %d", &a, &b);
g[a].push_back(b);
gr[b].push_back(a);
}
Запускаем
поиск в глубину на входном графе. Последовательность, в которой завершается
обработка вершин графа, сохраняется в массиве top.
used.resize(n);
for (i = 0; i < n; i++)
if (!used[i]) dfs1(i);
Запускаем
поиск в глубину на обратном графе. Вершины обратного графа рассматриваем в
порядке обхода массива top
справа налево (с конца в начало). Вершины, входящие в одну компоненту сильной
связности, красим одним и тем же цветом. Текущий цвет раскраски находится в
переменной с.
reverse(top.begin(), top.end());
c = 0;
for (int v : top)
if (color[v] == -1) dfs2(v, c++);
Переменная c содержит
количество компонент связности. Положим in[i] = 1, если для компоненты связности номер i нет входного ребра (и in[i] = 0 иначе).
Положим out[i] = 1, если для компоненты связности номер i нет исходящего ребра (и out[i] = 0 иначе).
out.assign(c, 1);
for (i = 0; i < g.size(); i++)
for (int to : g[i])
Если ребро
i → to соединяет разные компоненты связности, то для компоненты номер color[to] имеется входящее ребро, а для компоненты номер color[i] имеется исходящее ребро.
{
in[color[to]] = 0;
out[color[i]] = 0;
}
Подсчитываем
количество компонент, не имеющих входящих (с1)
и исходящих (с2) ребер.
c1
= c2 = 0;
for (i = 0; i < in.size(); i++)
{
if (in[i]) c1++;
if (out[i]) c2++;
}
Вычисляем и выводим
ответ.
if (c == 1) ans = 0; else ans = max(c1, c2);
printf("%d %d\n", c1, ans);
Java реализация
import java.util.*;
public class Main
{
static ArrayList<Integer>[] g, gr;
static int used[], color[], in[], out[];
static Vector<Integer> top = new Vector<Integer>();
static void
dfs1(int v)
{
used[v] = 1;
for(int i = 0; i < g[v].size(); i++)
{
int to = g[v].get(i);
if (used[to] == 0) dfs1(to);
}
top.add(v);
}
static void
dfs2(int v, int c)
{
color[v] = c;
for(int i = 0; i < gr[v].size(); i++)
{
int to = gr[v].get(i);
if (color[to] == -1) dfs2(to,c);
}
}
@SuppressWarnings("unchecked")
public static void main(String[] args)
{
Scanner con = new Scanner(System.in);
int n = con.nextInt();
int m = con.nextInt();
g = new ArrayList[n];
for(int i = 0; i < n; i++)
g[i] = new
ArrayList<Integer>();
gr = new ArrayList[n];
for(int i = 0; i < n; i++)
gr[i] = new
ArrayList<Integer>();
for (int i = 0; i < m; i++)
{
int a = con.nextInt();
int b = con.nextInt();
g[a].add(b);
gr[b].add(a);
}
used = new int[n];
for(int i = 0; i < n; i++)
if (used[i] == 0) dfs1(i);
color = new int[n];
Arrays.fill(color, -1);
int c = 0;
for(int i = 0; i < n; i++)
{
int v = top.get(n-i-1);
if (color[v] == -1) dfs2(v,c++);
}
in = new int[c];
Arrays.fill(in, 1);
out = new int[c];
Arrays.fill(out, 1);
for(int i = 0; i < g.length; i++)
for(int j = 0; j < g[i].size(); j++)
{
int to = g[i].get(j);
// check edge i -> j if they in the same scc.
if (color[i] != color[to])
{
in[color[to]] = 0;
out[color[i]] = 0;
}
}
int c1 = 0, c2 = 0;
for(int i = 0; i < in.length; i++)
{
if (in[i] == 1) c1++;
if (out[i] == 1) c2++;
}
int ans = 0;
if (c != 1) ans
= Math.max(c1,c2);
System.out.println(c1 + " " + ans);
con.close();
}
}